Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized (that is, represented as a diagonal matrix in some basis). This concept of diagonalization is relatively straightforward for operators on finite-dimensional spaces, but requires some modification for operators on infinite-dimensional spaces. In general, the spectral theorem identifies a class of linear operators that can be modelled by multiplication operators, which are as simple as one can hope to find. In more abstract language, the spectral theorem is a statement about commutative C*-algebras. See also spectral theory for a historical perspective.
Examples of operators to which the spectral theorem applies are self-adjoint operators or more generally normal operators on Hilbert spaces.
The spectral theorem also provides a canonical decomposition, called the spectral decomposition, eigenvalue decomposition, or eigendecomposition, of the underlying vector space on which the operator acts.
In this article we consider mainly the simplest kind of spectral theorem, that for a self-adjoint operator on a Hilbert space. However, as noted above, the spectral theorem also holds for normal operators on a Hilbert space.
Contents |
Finite-dimensional case
Hermitian matrices
We begin by considering a Hermitian matrix A on a finite-dimensional real or complex inner product space V with the standard Hermitian inner product; the Hermitian condition means
for all x, y elements of V.
An equivalent condition is that A* = A, where A* is the conjugate transpose of A. If A is a real matrix, this is equivalent to AT = A (that is, A is a symmetric matrix). The eigenvalues of a Hermitian matrix are real.
Recall that an eigenvector of a linear operator A is a (non-zero) vector x such that Ax = λx for some scalar λ. The value λ is the corresponding eigenvalue.
Theorem. There is an orthonormal basis of V consisting of eigenvectors of A. Each eigenvalue is real.
We provide a sketch of a proof for the case where the underlying field of scalars is the complex numbers.
By the fundamental theorem of algebra, applied to the characteristic polynomial, any square matrix with complex entries has at least one eigenvector. Now if A is Hermitian with eigenvector e1, we can consider the space K = span{e1}⊥, the orthogonal complement of e1. By Hermiticity, K is an invariant subspace of A. Applying the same argument to K shows that A has an eigenvector e2 ∈ K. Finite induction then finishes the proof.
The spectral theorem holds also for symmetric matrices on finite-dimensional real inner product spaces, but the existence of an eigenvector is harder to establish. A real symmetric matrix has real eigenvalues, therefore eigenvectors with real entries.
If one chooses the eigenvectors of A as an orthonormal basis, the matrix representation of A in this basis is diagonal. Equivalently, A can be written as a linear combination of pairwise orthogonal projections, called its spectral decomposition. Let
be the eigenspace corresponding to an eigenvalue λ. Note that the definition does not depend on any choice of specific eigenvectors. V is the orthogonal direct sum of the spaces Vλ where the index ranges over eigenvalues. Let Pλ be the orthogonal projection onto Vλ and λ1,..., λm the eigenvalues of A, one can write its spectral decomposition thus:
The spectral decomposition is a special case of the Schur decomposition. It is also a special case of the singular value decomposition.
For the infinite-dimensional case, A is a linear operator, and the spectral decomposition is given by the integral
where σ denotes the spectrum of A and P is a projection (i.e. idempotent) operator.
Normal matrices
The spectral theorem extends to a more general class of matrices. Let A be an operator on a finite-dimensional inner product space. A is said to be normal if A* A = A A*. One can show that A is normal if and only if it is unitarily diagonalizable: By the Schur decomposition, we have A = U T U*, where U is unitary and T upper-triangular. Since A is normal, T T* = T* T. Therefore T must be diagonal. The converse is also obvious.
In other words, A is normal if and only if there exists a unitary matrix U such that
where Λ is the diagonal matrix the entries of which are the eigenvalues of A. The column vectors of U are the eigenvectors of A and they are orthonormal. Unlike the Hermitian case, the entries of Λ need not be real.
Compact self-adjoint operators
In Hilbert spaces in general, the statement of the spectral theorem for compact self-adjoint operators is virtually the same as in the finite-dimensional case.
Theorem. Suppose A is a compact self-adjoint operator on a Hilbert space V. There is an orthonormal basis of V consisting of eigenvectors of A. Each eigenvalue is real.
As for Hermitian matrices, the key point is to prove the existence of at least one nonzero eigenvector. To prove this, we cannot rely on determinants to show existence of eigenvalues, but instead one can use a maximization argument analogous to the variational characterization of eigenvalues. The above spectral theorem holds for real or complex Hilbert spaces.
If the compactness assumption is removed, it is not true that every self adjoint operator has eigenvectors.
Bounded self-adjoint operators
The next generalization we consider is that of bounded self-adjoint operators on a Hilbert space. Such operators may have no eigenvalues: for instance let A be the operator of multiplication by t on L2[0, 1], that is
Theorem. Let A be a bounded self-adjoint operator on a Hilbert space H. Then there is a measure space (X, Σ, μ) and a real-valued measurable function f on X and a unitary operator U:H → L2μ(X) such that
where T is the multiplication operator:
This is the beginning of the vast research area of functional analysis called operator theory.
There is also an analogous spectral theorem for bounded normal operators on Hilbert spaces. The only difference in the conclusion is that now 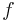 may be complex-valued.
may be complex-valued.
An alternative formulation of the spectral theorem expresses the operator  as an integral of the coordinate function over the operator's spectrum with respect to a projection-valued measure. When the normal operator in question is compact, this version of the spectral theorem reduces to the finite-dimensional spectral theorem above, except that the operator is expressed as a linear combination of possibly infinitely many projections.
as an integral of the coordinate function over the operator's spectrum with respect to a projection-valued measure. When the normal operator in question is compact, this version of the spectral theorem reduces to the finite-dimensional spectral theorem above, except that the operator is expressed as a linear combination of possibly infinitely many projections.
General self-adjoint operators
Many important linear operators which occur in analysis, such as differential operators, are unbounded. There is also a spectral theorem for self-adjoint operators that applies in these cases. To give an example, any constant coefficient differential operator is unitarily equivalent to a multiplication operator. Indeed the unitary operator that implements this equivalence is the Fourier transform; the multiplication operator is a type of Fourier multiplier.
See also
- Spectral theory
- Matrix decomposition
- Canonical form
- Jordan decomposition, of which the spectral decomposition is a special case.
- Singular value decomposition, a generalisation of spectral theorem to arbitrary matrices.
- Eigendecomposition of a matrix
References
- Sheldon Axler, Linear Algebra Done Right, Springer Verlag, 1997
- Paul Halmos, "What Does the Spectral Theorem Say?", American Mathematical Monthly, volume 70, number 3 (1963), pages 241–247


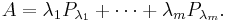
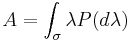

 = t \varphi(t). \;](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/108f59907f9c959f49ba7249ac612aff.png)
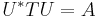
 = f(x) \varphi(x). \;](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/10951b7e8cc81821d2e7fc03a93b030e.png)